GameInference.jl

:warning: This repository was last tested with Julia 1.4.2.

This repository contains the implementation of a particle filtering technique for online inference of other player’s intentions in general-sum differential games. Two sources of intention uncertainty are considered:

Equilibrium uncertainty: Uncertainty about the equilibrium strategies that other players will employ to achieve a given objective.
Objective uncertainty: uncertainty about the objectives (cost functions in the differential game) of other players.

A thorough discussion of planning under equilibrium uncertainty alone can be found in [1]. Both sources of uncertainty are discussed in [2].

Usage

Installation

Clone this repository and its submodules:

git clone --recursive https://github.com/lassepe/GameInference.jl

In a Julia REPL from the project root type:

using Pkg
pkg"activate ."
# adding iLQGames.jl manually, since it is currently not registered.
pkg"add https://github.com/lassepe/iLQGames.jl"
pkg"instantiate"

Optional: In order to run experiments in parallel, make sure to start Julia with multiple threads. This setting can be verified from within the Julia REPL by looking at the output of Threads.nthreads().

Directory Layout

src/ contains the implementation of the particle filtering technique and related simulation code. The main file here is src/GameInference.jl which contains the module definition.
experiments/ contains the code for the experiments discussed in [1] and [2]. The main file here is experiments/main.jl
results/ contains the results of the experiments defined in experiments/main.jl. These results include both the raw data as *.csv files and the compiled evaluation plots as PDFs. Since this is a lot of data, results reside in a sperate repository which is included as a git submodule.

Running Simulation Experiments

The file expirments/main.jl contains the setup of experiments. Here, two types of experiments are considered:

Prediction experiments: The robot observes the interaction of multiple simulated humans and seeks to predict their future trajectory. The simulation and visualization routines for this class of experiments is implemented in experiments/prediction_experiment.jl
Planning experiments: The robot interacts with other players and seeks find a strategy which allows it to reach its goal efficiently. The simulation and visualization routines for this class of experiments is implemented in experiments/planning_experiment.jl.

Additionally, we distinguish two types of scenarios corresponding to the two sources of uncertainty outlined above:

Equilibrium uncertainty: Scenarios in which the robot has full knowledge of the human objectives but uncertainty still arises from the fact that the game admits multiple equilibria which human players may be operating at. The experiment setups for this scenario type is are stored in the variable experiment_setups_uneq.
Objective uncertainty: Scenarios in which the robot has incomplete knowledge of both (a) the human objectives, and (b) the human equilibrium preference given their objective.

The experiment setups for this scenario type are twofold:

experiment_setups_unprox: scenarios with uncertain proximity cost of human players, and
experiment_setups_ungoal: scenarios with uncertain goal positions of human players.

In order to run the experiments corresponding to these setups, call run_and_save_experiments on a collection of experiment setups, e.g. run_and_save_experiments(experiment_setups_uneq, result_dir), where result_dir represents the directory to which the results are to be written. For convenience, experiments/main.jl contains the methods run_unprox, run_unprox, run_unprox to perform these tasks for the predefined experiment setups.

Creating Plots

In order to visualize the results of an experiment, call the corresponding generate_plots_{uneq,unprox,ungoal} method. This method calls create_and_save_viz for each setup in experiment_setup_{uneq,unprox,ungoal}. In addition to the simulation experiments, this method renders a Monte Carlo study for the scenario type. The resulting plots are saved as PDFs to the provided data_dir.

Examples

Equilibrium Uncertainty: Inference-Based Strategy Alignment

The animation below shows an example of inference-based strategy alignment [1]. This example shows the interaction of five players; a single robot (blue, starting on the left) and four simulated humans. The dynamics of each player are those of a 4D-unicycle and each player wishes to reach their goal on the other side of the intersection while avoiding collisions with others. This problem can be cast as a general-sum differential game which can be solved to a non-cooperative equilibrium using linear-quadratic approximations. However, even if the objectives of all players are known, uncertainty still arises from the fact that there are multiple possible equilibrium solutions to this problem.

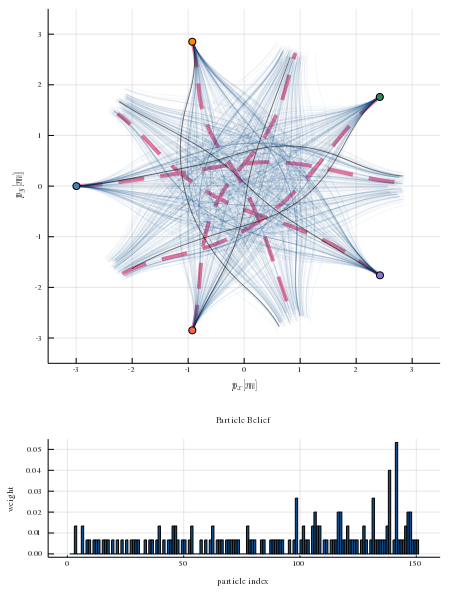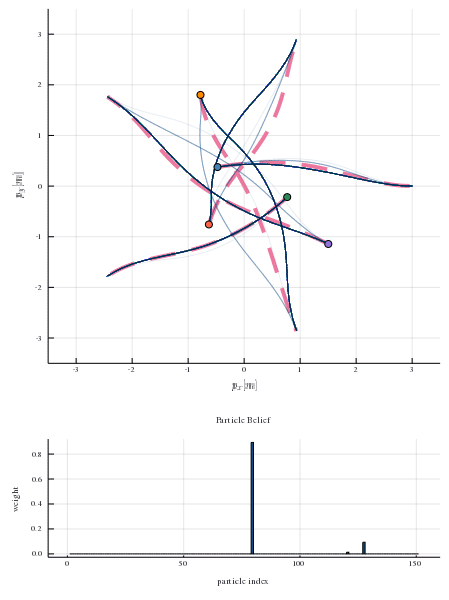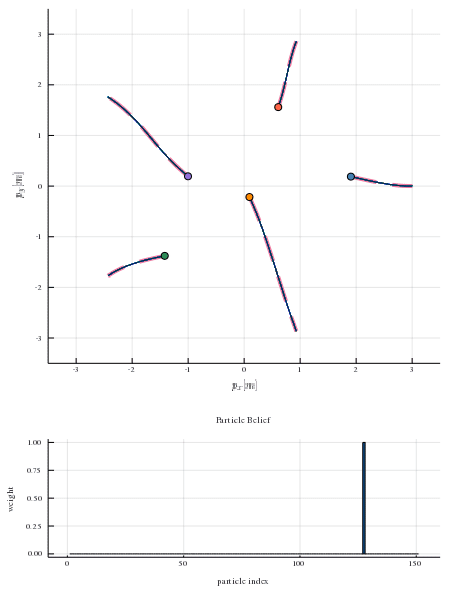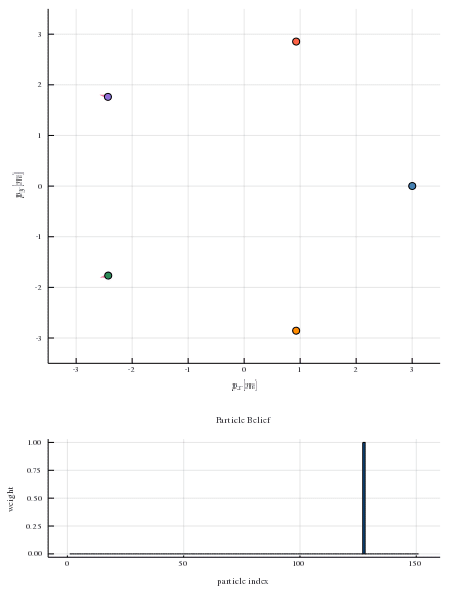
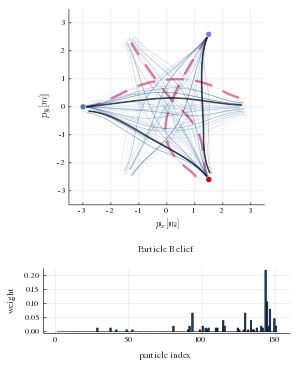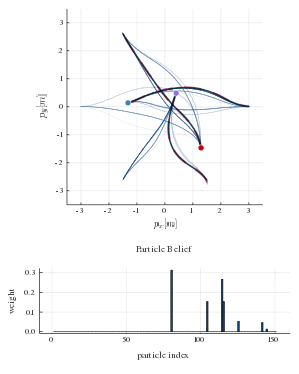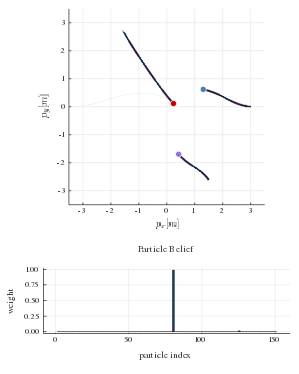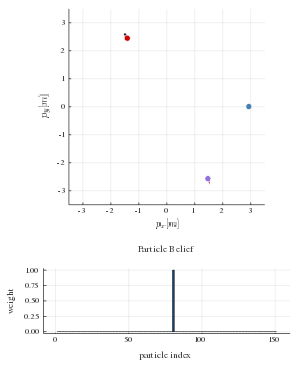
This repository provides a particle filtering techniques that admits to estimate the likelihood of different game solutions. Each particle corresponds to an equilibrium solution of the game and has a weight associated to it. In the figure below, the true human strategies are shown with red dashed lines and the strategies that comprise the particle belief are shown as blue transparent lines. The histogram below shows the distribution of weights in the particle belief. As the robot interacts with human players and observes their decisions, it can infer the likelihood of the sampled equilibrium solutions. At every time step, the robot invokes the strategy corresponding to the most likely game solution. After a few time steps the robot is able to recover the true human equilibrium preference. By aligning its own strategy to that equilibrium it allows everyone to reach their goal safely and efficiently.

Figure 1: Closed-loop interaction of a single robot (blue, starting left) with four simulated humans under *equilibrium uncertainty*. The robot uses equilibrium inference to align its strategy to the most likely human equilibrium preference.

Objective Uncertainty

In the example above, uncertainty only arises from the fact that there are multiple game solutions for a known objective. However, in practice, a robot may only have incomplete knowledge of the objectives of other players. This problem is thoroughly discussed in my Master’s thesis [2].

For illustration of this problem, consider the 3-player interaction example below. In this example, again, each player wishes to reach their goal on the other side of the intersection while avoiding collisions with others. However, in this example the robot does not know the exact goal location of the human players. Instead, it assumes a uniform distribution over two possible goal locations for each human: one in which the human goes straight, and one in which the human makes a left turn.

Note that for each of these possible objectives there are still multiple equilibria. Hence, in addition to inferring the human objectives (i.e. their goal positions) the robot also needs to recover the strategy that human will use to achieve their objective.

Figure 2: Closed-loop interaction of a single robot (blue, starting left) with two simulated humans under *objective uncertainty*. The robot uses inference to recover both, the unknown components of the human objectives (here, their goal position), as well as their equilibrium preference within that objective.

Trouble Shooting

Reducing the Startup Time: Pre-Compilation into a System Image

Some of the methods in iLQGames.jl require some significant amount of compilation for experiments with more players. Though compile times have certainly improved since v1.4, it is advisable to pre-compile some of the more compilation-heavy methods into a system image which can be loaded later to reduce startup times. This step is useful if you intend to run the experiments multiple times spread out over multiple sessions and wish to try out different experiment parameters (or modify the inference algorithm).

Note: If you only intend to try out this code for a single session, this step is not necessary!

Pre-compilation is done as follows.

Install the PackageCompiler if not already present on your system:

]add PackageCompiler

Compile the system image. This will create the system image precompile/ilqgames_dev.sysimg.so.

julia precompile/compile_systemimage.jl

For all experiments, launch Julia as follows to load the custom system image.
```
julia --sysimage ./precompile/ilqgames_dev.sysimg.so
```

Citation

[1] Inference-Based Strategy Alignment for General-Sum Differential Games

@inproceedings{peters2020InferenceBased,
  title = {Inference-Based Strategy Alignment for General-Sum Differential Games},
  booktitle = {International Conference on Autonomous Agents and Multi-Agent Systems (AAMAS)},
  author = {Peters, Lasse and Fridovich-Keil, David and Tomlin, Claire J. and
    Sunberg, Zachary N.},
  date = {2020}
}

[2] Accommodating Intention Uncertainty in General-Sum Games for Human-Robot Interaction

@thesis{peters2020Accommodating,
  title = {Accommodating Intention Uncertainty in General-Sum Games for Human-Robot
  Interaction},
  author = {Peters, Lasse},
  date = {2020},
  institution = {Hamburg University of Technology},
  type = {Master's thesis}
}