Lasse Peters

Contingency Games for Multi-Agent Interaction

Best Paper Award Finalist · IEEE RAS TC on Robot Control 2025

@article{peters2024ral,
  title={Contingency Games for Multi-Agent Interaction},
  author={Peters, Lasse and Bajcsy, Andrea and Chiu, Chih-Yuan and Fridovich-Keil, David and Laine, Forrest and Ferranti, Laura and Alonso-Mora, Javier},
  journal={IEEE Robotics and Automation Letters (RA-L)},
  year={2024},
}

Resources

Abstract

Contingency planning, wherein an agent generates a set of possible plans conditioned on the outcome of an uncertain event, is an increasingly popular way for robots to act under uncertainty. In this work we take a game-theoretic perspective on contingency planning, tailored to multi-agent scenarios in which a robot’s actions impact the decisions of other agents and vice versa. The resulting contingency game allows the robot to efficiently interact with other agents by generating strategic motion plans conditioned on multiple possible intents for other actors in the scene. Contingency games are parameterized via a scalar variable which represents a future time when intent uncertainty will be resolved. By estimating this parameter online, we construct a game-theoretic motion planner that adapts to changing beliefs while anticipating future certainty. We show that existing variants of game-theoretic planning under uncertainty are readily obtained as special cases of contingency games. Through a series of simulated autonomous driving scenarios, we demonstrate that contingency games close the gap between certainty-equivalent games that commit to a single hypothesis and non-contingent multi-hypothesis games that do not account for future uncertainty reduction.

Code

Released upon publication of the manuscript:

Backend

Beyond these repositories, our contingency game solver relies on the following packages, already open-sourced:

Additional Analyses

Interactive Demo

Contingency games are best understood via an interactive example. Below, we provide an interactive version of the example given in the video above: an autonomous robot encountering a jaywalking pedestrian.

By varying the sliders controlling the main parameters of the contingency game, we can build intuition for how the robot’s behavior changes as a function of the uncertainty in the pedestrian’s intent. In particular, observe that:

  • The robot balances the cost of each hypothesis according to the likelihood under the current belief.
  • The robot exploits the anticipated certainty to balance safety and efficiency.
  • At extreme values of the branching time, we recover established game-theoretic planning paradigms as a special case:
    • When the branching time is zero, the robot assumes full certainty and solves the certainty-equivalent problem.
    • When the branching time is equal to the planning horizon, the robot develops a single plan that minimizes expected cost under fixed uncertainty.

The effect of ϵ\epsilon on our branching time heuristic

The paper includes the following remark:

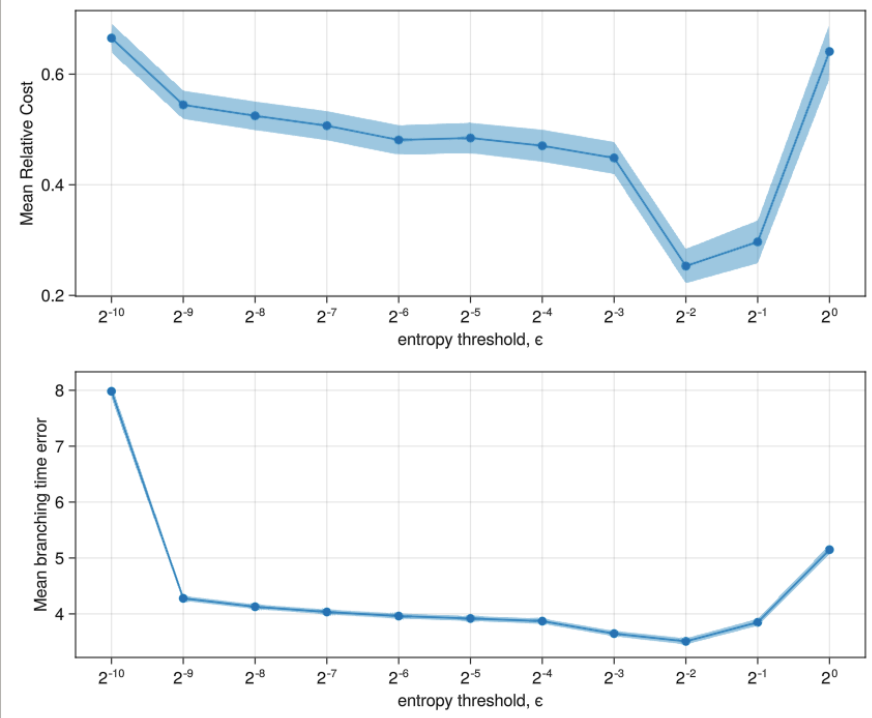
A low threshold results in more conservative behavior. As informed by a parameter sweep over ϵ\epsilon, we choose ϵ=2−2\epsilon = 2^{-2} for all experiments for best performance.

Below, we show the data underpinning this statement. This data was generated by running the receding-horizon Monte Carlo study for the crosswalk example at 11 different threshold values of ϵ\epsilon, namely, {20,2−1,2−2,⋯ ,2−10}\{2^0, 2^{-1}, 2^{-2}, \cdots, 2^{-10}\}. Note that we compute belief entropy with log-base ∣Θ∣|\Theta| = 2, so that 202^0 corresponds to a uniform initial belief.

epsilon ablation

Last Updated: 2023-11-12