Inference-Based Strategy Alignment for General-Sum Differential Games

News

• The code for this work is publicly available on GitHub
• This work has been accepted to AAMAS 2020.

Abstract

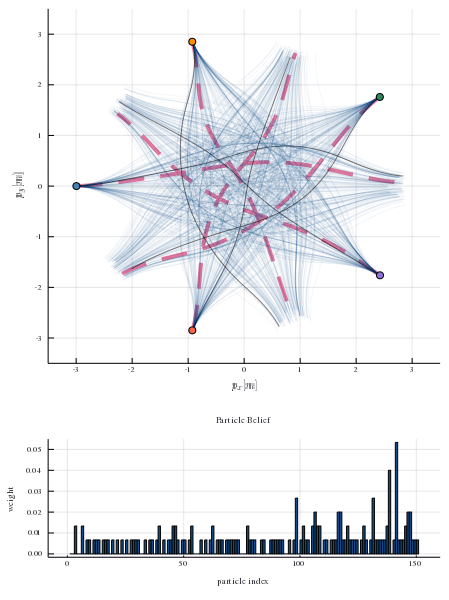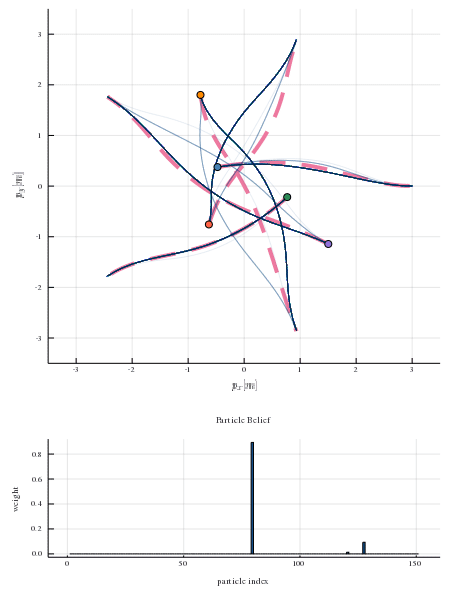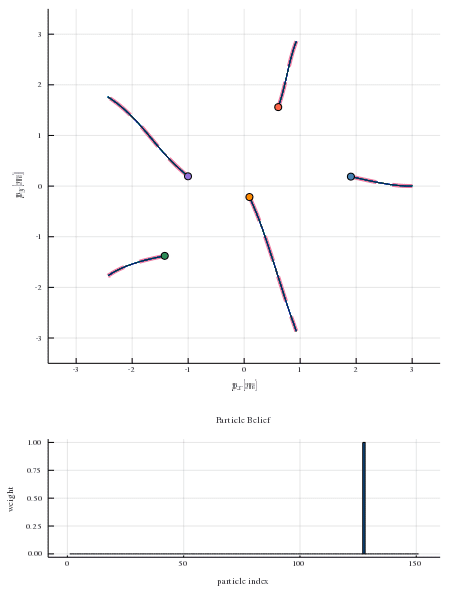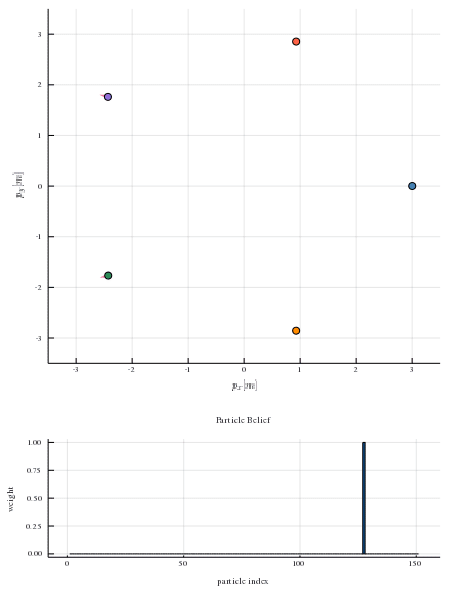
In many settings where multiple agents interact, the optimal choices for each agent depend heavily on the choices of the others. These coupled interactions are well-described by a general-sum differential game, in which players have differing objectives, the state evolves in continuous time, and optimal play may be characterized by one of many equilibrium concepts, e.g., a Nash equilibrium. Often, problems admit multiple equilibria. From the perspective of a single agent in such a game, this multiplicity of solutions can introduce uncertainty about how other agents will behave. This paper proposes a general framework for resolving ambiguity between equilibria by reasoning about the equilibrium other agents are aiming for. We demonstrate this framework in simulations of a multi-player human-robot navigation problem that yields two main conclusions: First, by inferring which equilibrium humans are operating at, the robot is able to predict trajectories more accurately, and second, by discovering and aligning itself to this equilibrium the robot is able to reduce the cost for all players.